Optical density, normalization, and growth rates

Background on optical density

The interaction of light within samples of suspended microorganisms will differ from light passing through concentrated solutions. Instead of being absorbed, light is scattered by the cells in suspension. This scattered light is measured as optical density (OD). As turbidity increases, more scattering occurs, resulting in a higher OD reading.

tip

Looking to calibrate for OD600 readings? Visit this page.

Normalization

Due to manufacturing variables such as differences in LED strength and sensitivity, the raw OD readings can't be compared against each other. Instead, we use the normalization technique described below:

A series of initial OD readings are averaged to produce a reference value (denominator). New OD readings after the reference value are normalized using the following simple equation:

$$\frac{\normalsize \text{latest\thickspace OD}}{\normalsize \text{reference\thickspace OD}}=\text{normalized\thickspace OD}$$

For example:

Pioreactor name	Reference OD	Latest OD
Pioreactor1	0.030	0.033
Pioreactor2	0.010	0.015

It's difficult to compare raw OD readings since the starting values are different. However, if we normalize using the above equation:

Pioreactor1

$\frac{\small 0.033}{\small 0.030}=1.1$

Culture growth by 1.1x.

Pioreactor2

$\frac{\small 0.015}{\small 0.010}=1.5$

Culture growth by 1.5x.

We can more accurately compare culture growth using these ratios as opposed to using the raw OD values.

tip

Because of the way we defined normalized optical density, it has the following easy interpretation: its the multiplicative amount the culture has changed by. So if the normalized OD is 2.0, the culture has doubled its initial concentration, i.e. doubled the population since the volume is fixed. This also works for traditional OD600 measurements: if your initial sample has OD600 equal to 0.45, then a normalized OD of 2.0 is the same as an OD600 of twice that, or 0.90. (Generally...).

Blanking

While basic normalization accounts for initial OD differences, it does not consider the optical density of the media itself. For a more accurate growth rate calculation, you can blank your sample.

Blanking your vials is recommended for experiments that begin with low OD readings (ex. inoculating small amounts of yeast). By blanking, you are able to observe the OD of only the microorganism of interest.

As an example, let's consider the same data as above, but this time we have information on the blank ODs:

Pioreactor name	Blank OD (media)	Reference OD (media with culture)	Difference (reference - blank)	Latest OD
Pioreactor1	0.025	0.030	0.005	0.033
Pioreactor2	0.005	0.010	0.005	0.015

We can now subtract the blank values from the latest OD and reference OD values:

$$\frac{\normalsize \text{latest\thickspace OD}-\text{blank\thickspace OD}}{\normalsize \text{reference\thickspace OD}-\text{blank\thickspace OD}}=\text{blanked\thickspace normalized\thickspace OD}$$

Pioreactor1

$\frac{\small 0.033-0.025}{\small 0.030-0.025}=1.6x$

Culture growth by 1.6x.

Pioreactor2

$\frac{\small 0.015-0.005}{\small 0.010-0.005}=2x$

Culture growth by 2x.

By accounting for the OD of the blank media, we are able to calculate a more accurate growth rate.

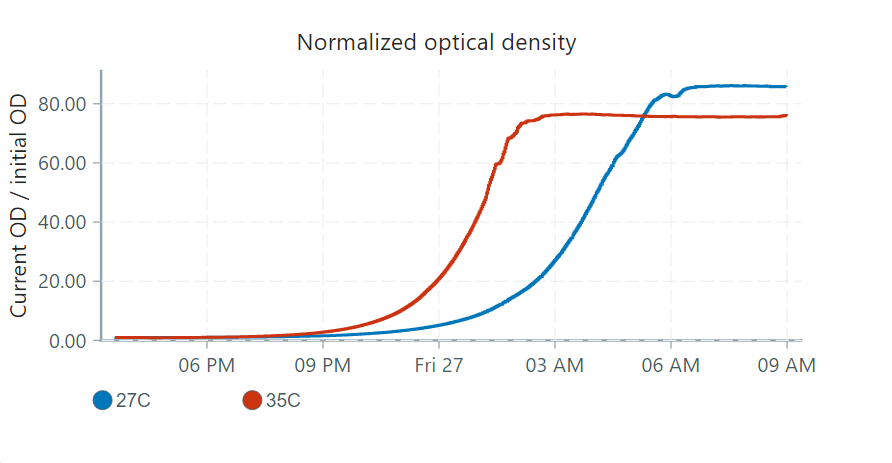
Growth rate

We inoculated two vials with a drop of re-hydrated yeast, and tracked their growth at temperatures 27°C and 35°C. The following normalized optical density chart was generated by the Pioreactor:

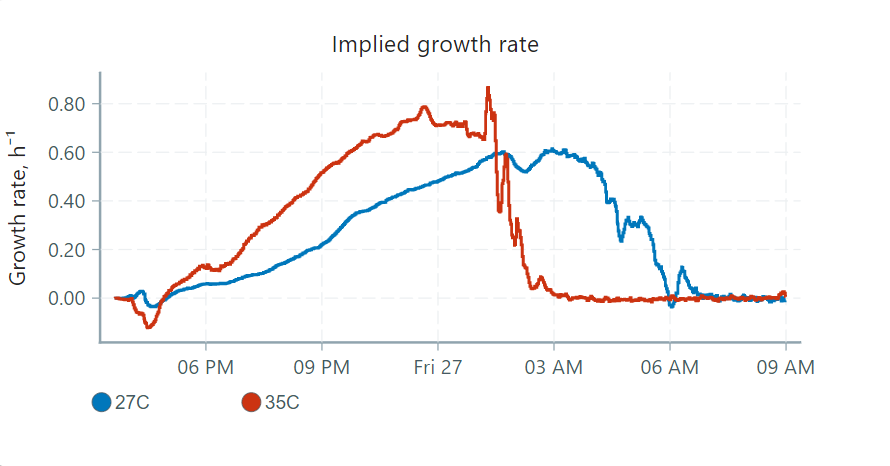
From the normalized optical density, an implied growth rate graph is generated. The relationship between the implied growth rate, $\text{gr}$ and the normalized optical density, $\text{nOD}$ is exponential, defined by the following equation:

$$\text{nOD}(t) = \exp{ \left( \int_0^t \text{gr}(s)ds \right)}$$

We can rewrite this equation in terms of the growth rate:

$$\text{gr}(t)= \frac{ \text{nOD}'(t)} {\text{nOD}(t)}$$

which plainly states that the growth rate is the rate of change of the size of the culture, normalized by the size of the culture.

This rate can give insight on the state of your culture under different external conditions.

These graphs can be interpreted in 4 phases:

• The lag phase: No observed growth, but high cell activity. In this stage, cells are in a nutrient rich environment and are preparing for growth by synthesizing proteins and other necessary molecules.
• Exponential (or log) phase: Cells are now dividing and doubling in numbers after each generation time. Generation times are dependent on the species you are using for your experiment.
• Stationary phase: Eventually the growth of cells reaches a plateau as nutrients are used up and waste products accumulate. At this point, the number of dividing cells will equal the number of dying cells.
• Decline (or death) phase: As nutrients are depleted, cell growth slows while cell death increases.

Here's how these phases would apply to our graphs, focusing on the 35°C vial:

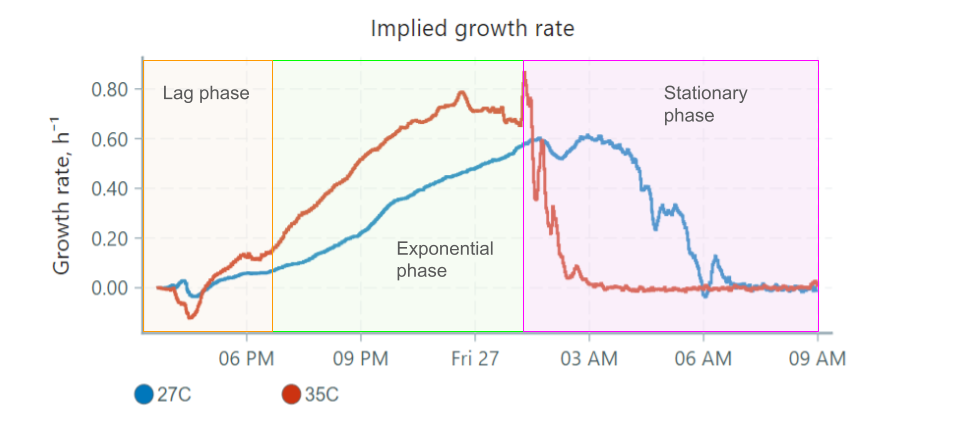
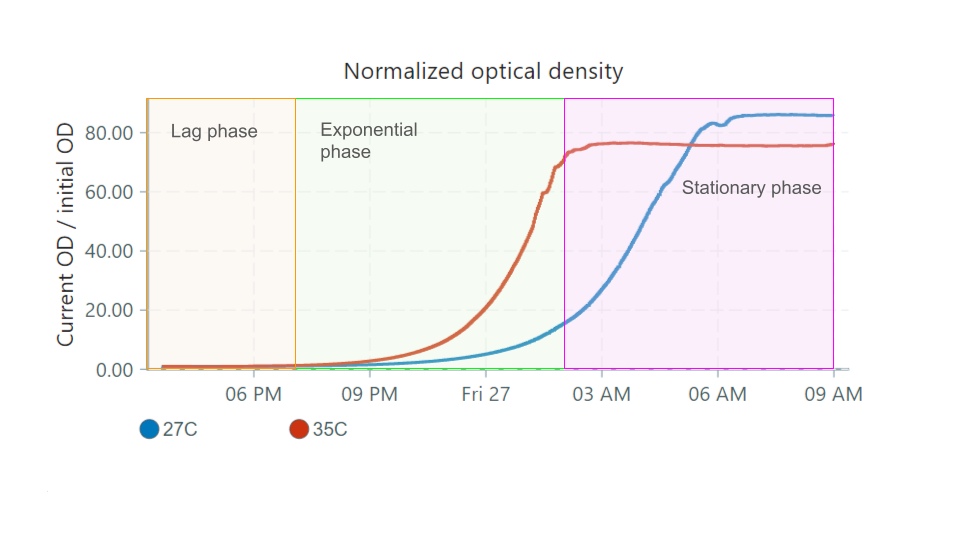
Some things to note:

• The lag phase can be detected easily in the growth rate graph, as the rate is stable and doesn't begin increasing until a bit after 6 PM. This is not easily determined in the nOD graph, since at this point the overall turbidity of the culture is low.
• The exponential phase occurs when the growth rate is high/increasing.
• When the culture reaches the stationary phase, growth rate drops to 0 since the culture is no longer growing in size. The turbidity is constant.
• The decline phase is not represented in the graphs above, as yeast remain in the stationary phase over many days.